How to check whether a binary tree is height balanced or not?

A height balanced binary tree is a binary tree in which the height of the left subtree and right subtree of any node does not differ by more than 1 and both the left and right subtree are also height balanced.

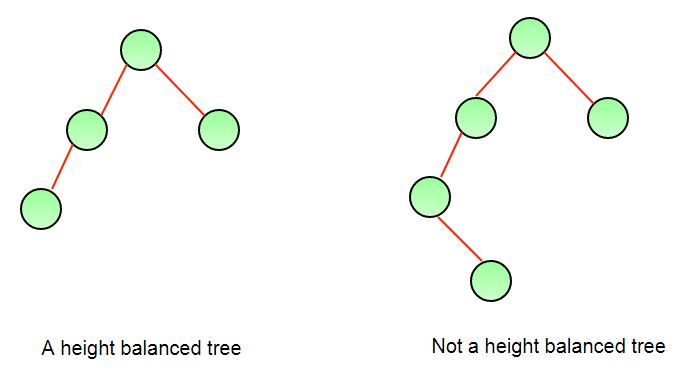
Examples: The tree on the left is a height balanced binary tree. Whereas the tree on the right is not a height balanced tree. Because the left subtree of the root has a height which is 2 more than the height of the right subtree.
 

Naive Approach: To check if a tree is height-balanced:

Get the height of left and right subtrees using dfs traversal. Return true if the difference between heights is not more than 1 and left and right subtrees are balanced, otherwise return false. 

Below is the implementation of the above approach.

Output

Tree is not balanced

Time Complexity: O(n^2) in case of full binary tree.
Auxiliary Space: O(n) space for call stack since using recursion

Efficient implementation: Above implementation can be optimized by 

Calculating the height in the same recursion rather than calling a height() function separately. 

• For each node make two recursion calls – one for left subtree and the other for the right subtree. 
• Based on the heights returned from the recursion calls, decide if the subtree whose root is the current node is height balanced or not. 
• If it is balanced then return the height of that subtree. Otherwise, return -1 to denote that the subtree is not height balanced.

Below is the implementation of the above approach.

Output

Balanced

Time Complexity: O(n) 

• Because we are only one dfs call and utilizing the height returned from that to determine the height balance, it is performing the task in linear time.

Auxiliary Space: O(n)